Gallery¶
Sample plots generated with the latest version of the library directly from the code when the documentation is built.
Images¶
Preamble¶
Auxiliar methods pyplot.gallery._utils._set_plot_labels() and pyplot.gallery._utils._set_plot_limits()
are used to make the gallery code uniform.
from matplotlib import pyplot as plt
def _set_plot_labels():
ax = plt.gca()
ax.set(
xlabel='x [m]',
ylabel='y [m]',
zlabel='z [m]'
)
def _set_plot_limits(lmin: float = -0.5, lmax: float = 0.5):
ax = plt.gca()
ax.set(
xlim=[lmin, lmax],
ylim=[lmin, lmax],
zlim=[lmin, lmax]
)
Poses¶
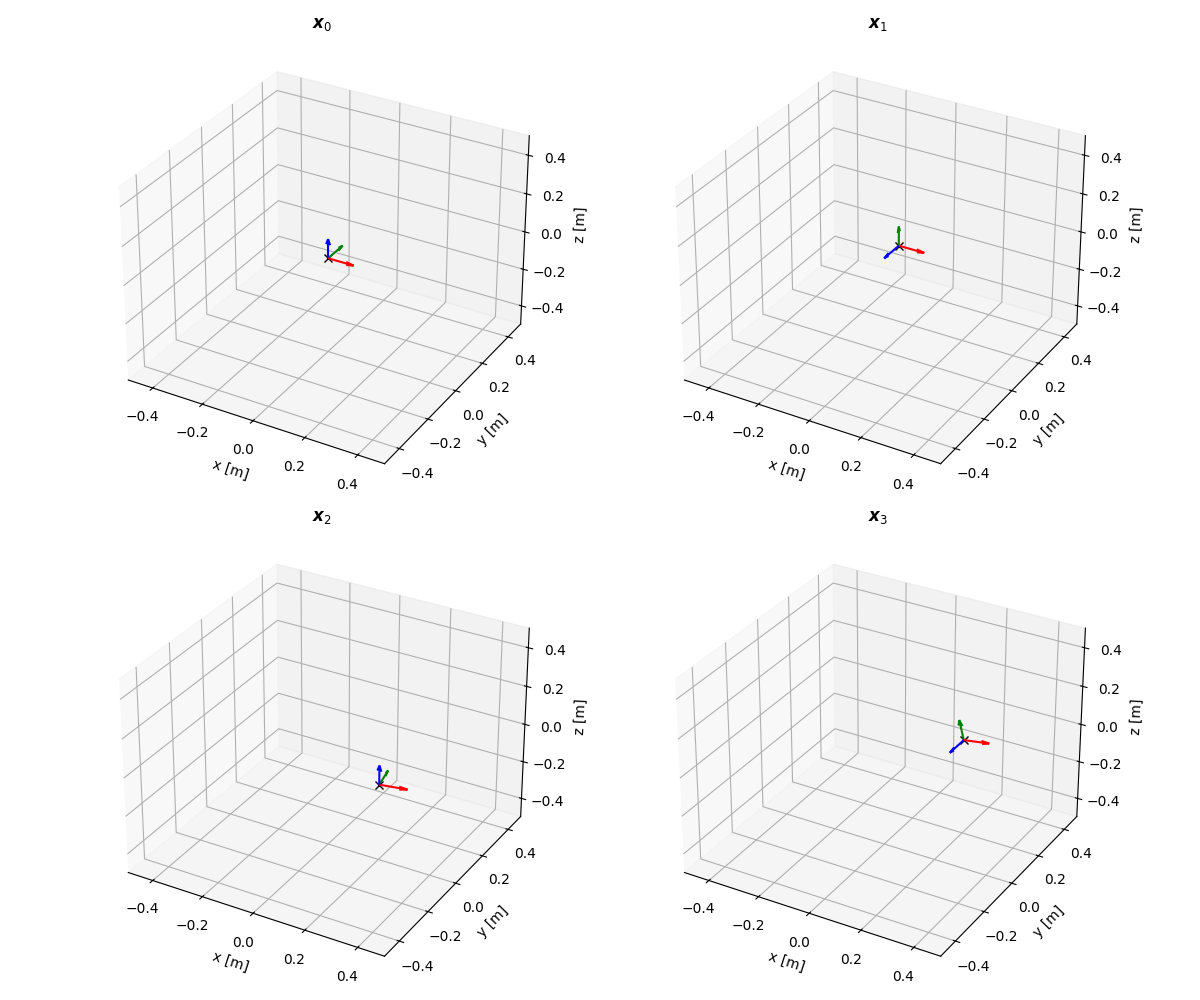
Generated by
from dqrobotics import *
# Adding the prefix `dqp` to help users differentiate from `plt`
import dqrobotics_extensions.pyplot as dqp
from ._utils import _set_plot_labels, _set_plot_limits
from matplotlib import pyplot as plt
from math import sin, cos, pi
def output_poses():
"""
Calculate and visualize multiple poses represented as DQs.
"""
# x1
t1 = 0
r1 = 1
x1 = r1 + 0.5 * E_ * t1 * r1
# x2
t2 = 0.1 * j_
r2 = cos(pi / 4) + i_ * sin(pi / 4)
x2 = r2 + 0.5 * E_ * t2 * r2
# x3
t3 = - 0.1 * k_ + 0.2 * i_
r3 = cos(pi / 32) + k_ * sin(pi / 32)
x3 = r3 + 0.5 * E_ * t3 * r3
# x4
x4 = x1 * x2 * x3
# Plot using subplot
fig = plt.figure(figsize=(12, 10))
pose_list = [x1, x2, x3, x4]
for i in range(0, len(pose_list)):
x = pose_list[i]
ax = plt.subplot(2, 2, i+1, projection='3d')
dqp.plot(x)
ax.title.set_text(rf'$\boldsymbol{{x}}_{i}$')
_set_plot_labels()
_set_plot_limits()
fig.tight_layout()
plt.savefig("output_poses.png")
Lines¶
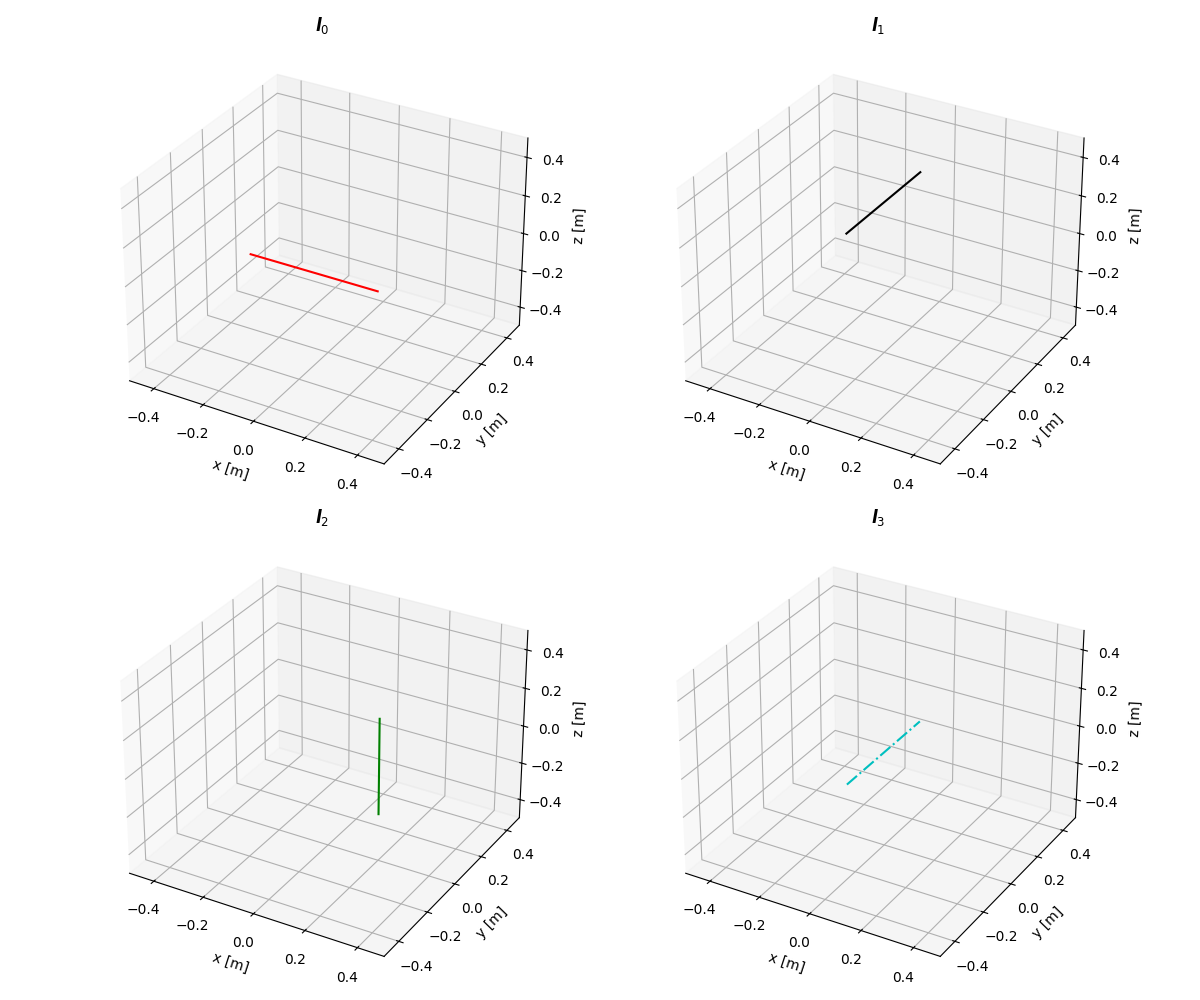
Generated by
from dqrobotics import *
# Adding the prefix `dqp` to help users differentiate from `plt`
import dqrobotics_extensions.pyplot as dqp
from ._utils import _set_plot_labels, _set_plot_limits
from matplotlib import pyplot as plt
def output_lines():
"""
Calculate and visualize multiple lines represented as DQs.
"""
# l1
l1 = i_
m1 = cross(-0.1 * j_, l1)
l1_dq = l1 + E_ * m1
# l2
l2 = j_
m2 = cross(0.3 * k_, l2)
l2_dq = l2 + E_ * m2
# l3
l3 = k_
m3 = cross(0.2 * i_, l3)
l3_dq = l3 + E_ * m3
# l4
l4 = j_
m4 = 0
l4_dq = l4 + E_ * m4
# Plot using subplot
fig = plt.figure(figsize=(12, 10))
line_list = [l1_dq, l2_dq, l3_dq, l4_dq]
color_list = ['r-', 'k-', 'g-', 'c-.']
for i in range(0, len(line_list)):
l_dq = line_list[i]
color = color_list[i]
ax = plt.subplot(2, 2, i+1, projection='3d')
dqp.plot(l_dq, line=True, scale=0.5, color=color)
ax.title.set_text(rf'$\boldsymbol{{l}}_{i}$')
_set_plot_labels()
_set_plot_limits()
fig.tight_layout()
plt.savefig("output_lines.png")
Planes¶
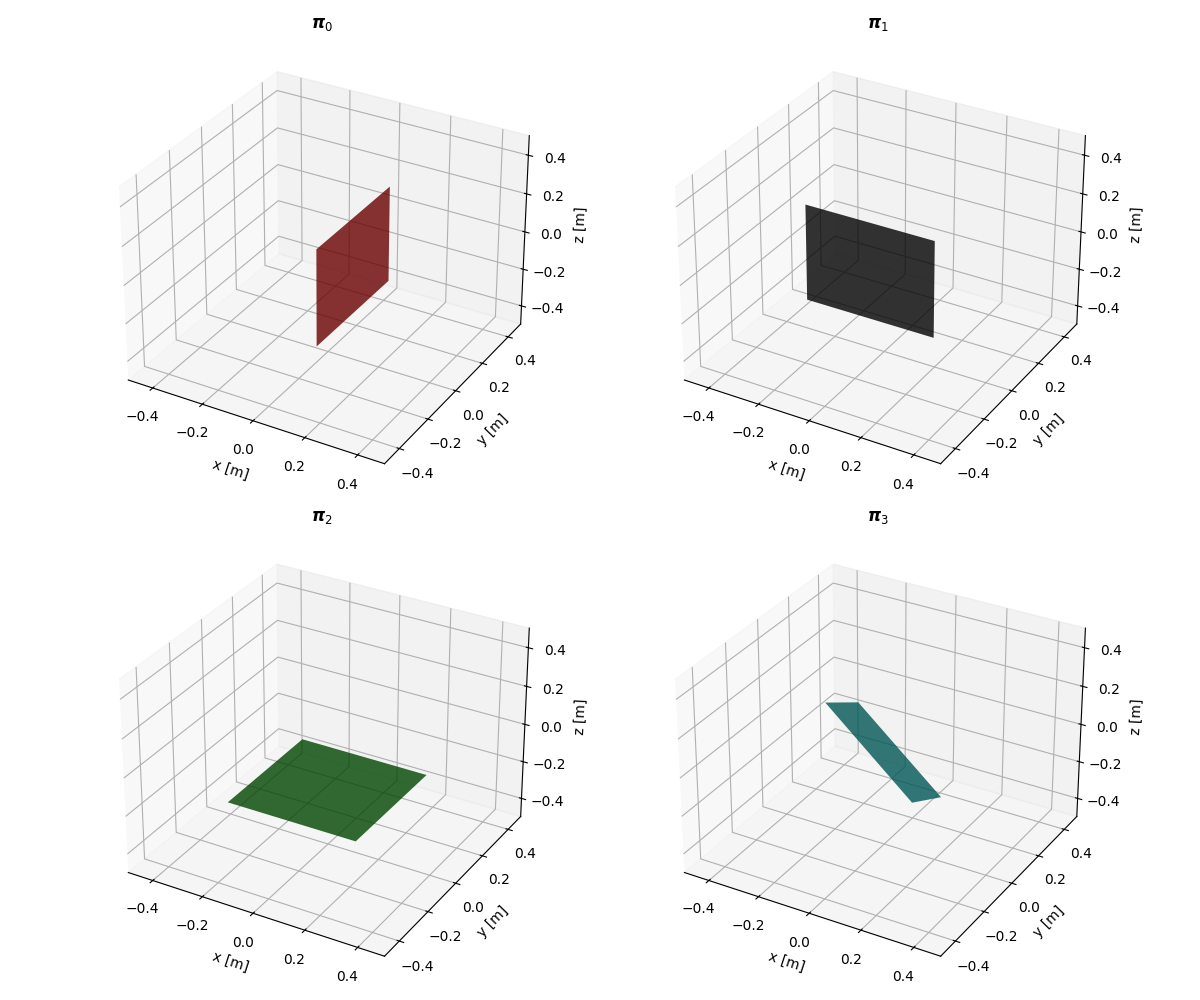
Generated by
from dqrobotics import *
# Adding the prefix `dqp` to help users differentiate from `plt`
import dqrobotics_extensions.pyplot as dqp
from ._utils import _set_plot_labels, _set_plot_limits
from matplotlib import pyplot as plt
def output_planes():
"""
Calculate and visualize multiple planes represented as DQs.
"""
# pi1
n1_pi = i_
d1_pi = 0.1
pi1_dq = n1_pi + E_ * d1_pi
# pi2
n2_pi = j_
d2_pi = -0.1
pi2_dq = n2_pi + E_ * d2_pi
# pi3
n3_pi = -k_
d3_pi = 0.2
pi3_dq = n3_pi + E_ * d3_pi
# pi4
n4_pi = normalize(i_ + j_ + k_)
d4_pi = 0
pi4_dq = n4_pi + E_ * d4_pi
# Plot using subplot
fig = plt.figure(figsize=(12, 10))
plane_list = [pi1_dq, pi2_dq, pi3_dq, pi4_dq]
color_list = ['r', 'k', 'g', 'c']
for i in range(0, len(plane_list)):
pi_dq = plane_list[i]
color = color_list[i]
ax = plt.subplot(2, 2, i+1, projection='3d')
dqp.plot(pi_dq, plane=True, scale=0.5, color=color)
ax.title.set_text(rf'$\boldsymbol{{\pi}}_{i}$')
_set_plot_labels()
_set_plot_limits()
fig.tight_layout()
plt.savefig("output_planes.png")
Spheres¶
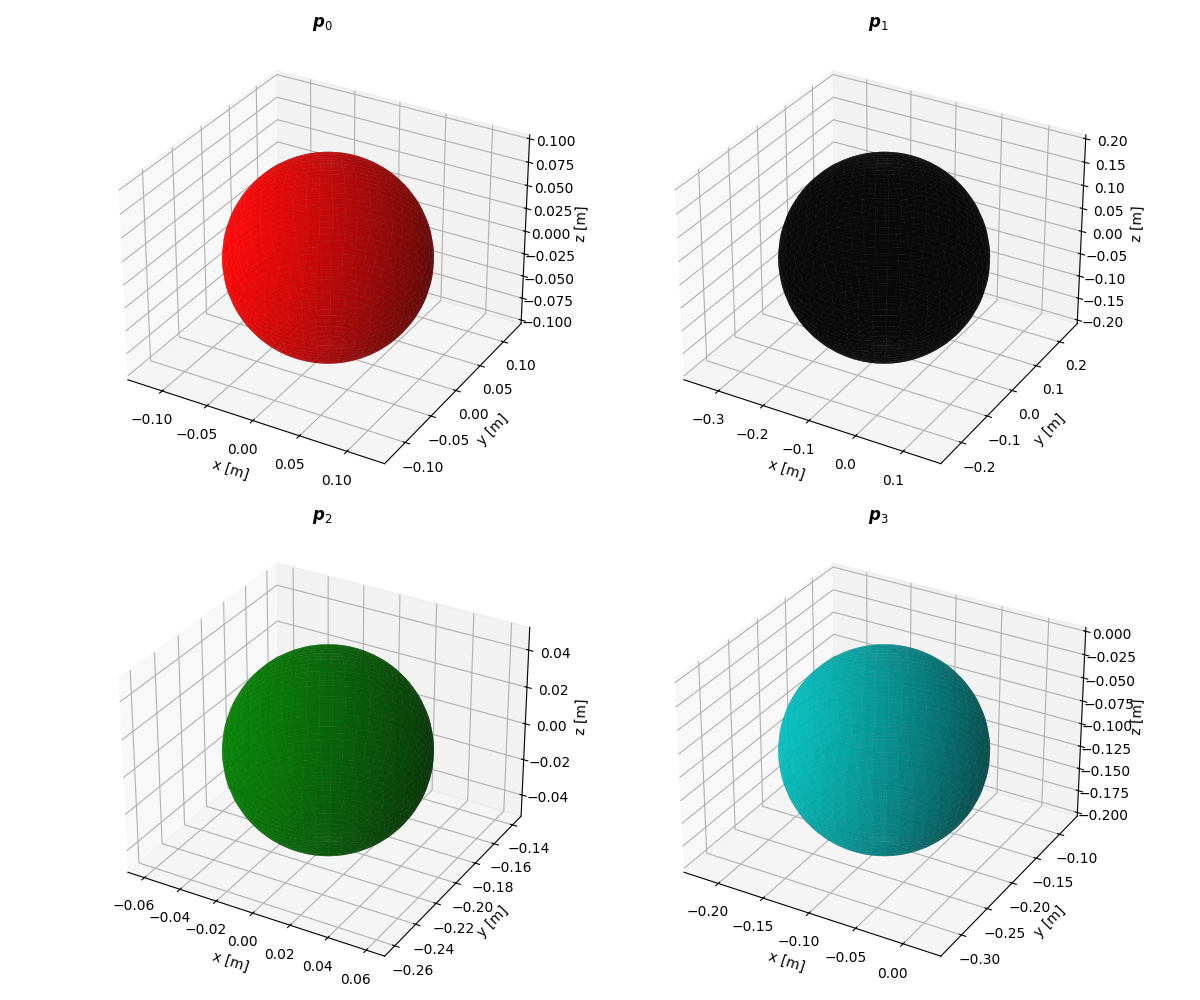
Generated by
from dqrobotics import *
# Adding the prefix `dqp` to help users differentiate from `plt`
import dqrobotics_extensions.pyplot as dqp
from ._utils import _set_plot_labels, _set_plot_limits
from matplotlib import pyplot as plt
def output_spheres():
"""
Calculate and visualize multiple spheres represented as DQs.
"""
# p1
p1 = DQ([0])
r1 = 0.1
# l2
p2 = 0.1*i_
r2 = 0.2
# l3
p3 = 0.2*j_
r3 = 0.05
# l4
p4 = 0.1*i_ + 0.2*j_ + 0.1*k_
r4 = 0.1
# Plot using subplot
fig = plt.figure(figsize=(12, 10))
sphere_list = [(p1, r1), (p2, r2), (p3, r3), (p4, r4)]
color_list = ['r', 'k', 'g', 'c']
for i in range(0, len(sphere_list)):
p, r = sphere_list[i]
color = color_list[i]
ax = plt.subplot(2, 2, i + 1, projection='3d')
dqp.plot(p, sphere=True, radius=r, color=color)
ax.title.set_text(rf'$\boldsymbol{{p}}_{i}$')
_set_plot_labels()
# https://matplotlib.org/stable/gallery/subplots_axes_and_figures/axis_equal_demo.html
ax.axis('equal') # Adjusted to show that they are spheres not ellipsoids
fig.tight_layout()
plt.savefig("output_spheres.png")
Videos¶
Moving primitives¶
Generated by
from dqrobotics import *
# Adding the prefix `dqp` to help users differentiate from `plt`
import dqrobotics_extensions.pyplot as dqp
from ._utils import _set_plot_labels, _set_plot_limits
from matplotlib import pyplot as plt
import matplotlib.animation as anm # Matplotlib animation
from functools import partial # Need to call functions correctly for matplotlib animations
from math import sin, cos
import numpy as np
def output_moving_primitives():
"""
Calculate and visualize multiple moving primitives represented as DQs.
"""
# Sampling time [s]
tau = 0.01
# Simulation time [s]
time_final = 1
# Store the plotted variables
stored_x = []
stored_l_dq = []
stored_pi_dq = []
stored_time = []
x = DQ([1])
ls_dq_init = [i_, j_, k_]
pis_dq_init = [k_, normalize(i_ + j_), normalize(i_ + j_ + k_)]
# Translation controller loop.
for time in np.arange(0, time_final + tau, tau):
# Modify line
ls_dq = [Ad(x, l_dq_init) for l_dq_init in ls_dq_init]
pis_dq = [Adsharp(x, pi_dq_init) for pi_dq_init in pis_dq_init]
# Store data for posterior animation
stored_x.append(x)
stored_l_dq.append(ls_dq)
stored_pi_dq.append(pis_dq)
stored_time.append(time)
# Move x
r = cos((10 * time) / 2) + j_ * sin((10 * time) / 2)
t = 0.1*(i_ + j_ + k_) * sin(time)
x = r + 0.5 * E_ * t * r
def animate_plot(n, stored_x, stored_l_dq, stored_pi_dq, stored_time):
plt.cla()
_set_plot_limits()
_set_plot_labels()
plt.title(f'Animation time={stored_time[n]:.2f} s out of {stored_time[-1]:.2f} s')
dqp.plot(stored_x[n])
line_colors = ['r+-', 'k.-', 'g+-', 'c-.']
plane_colors = ['r', 'k', 'g', 'c']
for line_counter in range(len(stored_l_dq[n])):
l_dq = stored_l_dq[n][line_counter]
dqp.plot(l_dq, line=True, scale=1, color=line_colors[line_counter % len(line_colors)])
for plane_counter in range(len(stored_pi_dq[n])):
pi_dq = stored_pi_dq[n][plane_counter]
dqp.plot(pi_dq, plane=True, scale=1, color=plane_colors[plane_counter % len(plane_colors)], alpha=0.2)
# Set up the plot
fig = plt.figure(dpi=200, figsize=(12, 10))
plt.axes(projection='3d')
anim = anm.FuncAnimation(fig,
partial(animate_plot,
stored_x=stored_x,
stored_l_dq=stored_l_dq,
stored_pi_dq=stored_pi_dq,
stored_time=stored_time),
frames=len(stored_x))
anim.save("output_moving_primitives.mp4")
Moving DQ_SerialManipulator s¶
Generated by
from dqrobotics import *
# Adding the prefix `dqp` to help users differentiate from `plt`
import dqrobotics_extensions.pyplot as dqp
from dqrobotics.robots import KukaLw4Robot
from dqrobotics.utils.DQ_Math import deg2rad
from ._utils import _set_plot_labels, _set_plot_limits
from matplotlib import pyplot as plt
import matplotlib.animation as anm # Matplotlib animation
from functools import partial # Need to call functions correctly for matplotlib animations
import numpy as np
from math import pi, cos, sin
def output_moving_manipulators():
"""
Calculate and visualize multiple moving primitives represented as DQs.
"""
# Animation function
def animate_robots(n, robots, stored_qs, stored_time):
"""
Create an animation function compatible with `plt`.
Adapted from https://marinholab.github.io/OpenExecutableBooksRobotics//lesson-dq8-optimization-based-robot-control.
:param n: The frame number, necessary for `pyplot`.
:param robots: The `DQ_SerialManipulator` tuple instance to plot.
:param stored_qs: The sequence of joint configurations.
:param stored_time: The sequence of timepoints to plot in the title.
"""
plt.cla()
_set_plot_limits(-0, 1.0)
_set_plot_labels()
plt.title(f'Joint control time={stored_time[n]:.2f} s out of {stored_time[-1]:.2f} s')
R1, R2 = robots
dqp.plot(R1, q=stored_qs[n][0],
line_color='r',
line_width=5,
cylinder_color="k",
cylinder_alpha=0.9,
cylinder_radius=0.035,
cylinder_height=0.1)
dqp.plot(R2, q=stored_qs[n][1],
line_color='b',
cylinder_color="c",
cylinder_alpha=0.3)
# Define the robots
R1 = KukaLw4Robot.kinematics()
R1.set_reference_frame(cos(pi/2) + k_*sin(pi/2))
R2 = KukaLw4Robot.kinematics()
R2.set_reference_frame(1 + 0.5*E_*(0.75*i_ + 0.75*j_))
# Sampling time [s]
tau = 0.01
# Simulation time [s]
time_final = 1
# Initial joint values [rad]
q1 = deg2rad([0, 45, 0, -45, 0, 45, 0])
q2 = q1
# Store the control signals
stored_qs = []
stored_time = []
# Translation controller loop.
for time in np.arange(0, time_final + tau, tau):
# Store data for posterior animation
stored_qs.append((q1, q2))
stored_time.append(time)
# Joint-space velocities
u1 = np.ones(7)
u2 = -0.1 * np.ones(7)
# Move the robots
q1 = q1 + u1 * tau
q2 = q2 + u2 * tau
# Set up the plot
fig = plt.figure(dpi=200, figsize=(12, 10))
plt.axes(projection='3d')
anim = anm.FuncAnimation(fig,
partial(animate_robots,
robots=(R1, R2),
stored_qs=stored_qs,
stored_time=stored_time),
frames=len(stored_qs))
anim.save("output_moving_manipulators.mp4")