L4 Differential Kinematics

License: CC-BY-NC-SA 4.0

Author: Murilo M. Marinho (murilo.marinho@manchester.ac.uk)

Pre-requisites for the learner¶

The user of this notebook is expected to have prior knowledge in

All the content and pre-requisites of lessons 1, 2, and 3.

I found an issue¶

Thank you! Please report it at https://github.com/MarinhoLab/OpenExecutableBooksRobotics/issues

Latex Macros¶

$\providecommand{\myvec}[1]{{\mathbf{\boldsymbol{{#1}}}}}$ $\providecommand{\mymatrix}[1]{{\mathbf{\boldsymbol{{#1}}}}}$

\providecommand{\myvec}[1]{{\mathbf{\boldsymbol{{#1}}}}}
\providecommand{\mymatrix}[1]{{\mathbf{\boldsymbol{{#1}}}}}

Package installation¶

%%capture
%pip install numpy
%pip install numpy --break-system-packages

Imports¶

import numpy as np
from math import pi, sin, cos

Suggested exercises¶

What about if the robot had 3 degrees-of-freedom, that is RRR?
What about if the robot had n degrees-of-freedom? Would it be much more complicated to solve?
What if the robot has one or more prismatic joints?

2 DoF planar robot (RR)¶

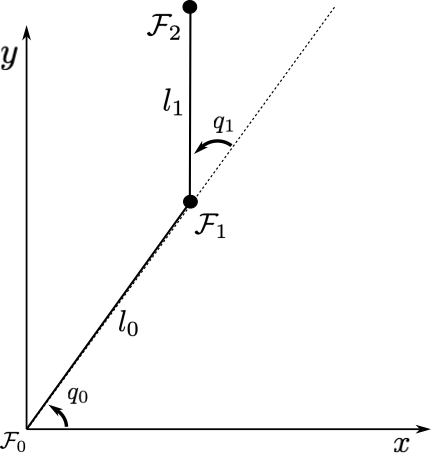
For the 2-DoF planar robot shown in the figure, let $q_0\triangleq q_0(t)$ , $q_1\triangleq q_1(t)$ , $l_{0}$ , $l_{1} \in \mathbb{R}$ be the parameters to calculate

\mymatrix{H}^{0}_{2}( q_0, l_{0},q_1,l_{1}) \in SE(2),

(1)

that is, the forward kinematics model of the 2 DoF planar manipulator with configuration space given by

\myvec{q} = \left[\begin{array}{ccc} q_0 \\ q_1 \end{array}\right].

(2)

Calculate the analytical Jacobian such that

\dot{\myvec{x}}=\mymatrix{J} \dot{\myvec{q}}

(3)

where

\myvec{x} = \left[\begin{array}{ccc} p_{x} \\ p_{y} \\ \phi_{z} \end{array}\right],

(4)

in which $p_{x}$ , $p_{y}$ , and $\phi_{z}$ are, respectively, the $x$ -axis position, the $y$ -axis position, and the $z$ -axis angle of $\mathcal{F}_{2}$ . Notice that $\dot{l}_{0}=\dot{l}_{1}=0$ .

For the same values of $\myvec{q}$ , calculate $\dot{\myvec{x}}$ when

\dot{\myvec{q}} = \left[\begin{array}{ccc} 5 \\ 10 \end{array}\right].

(5)

Step 1: Calculate the forward kinematics by hand¶

It is not possible to calculate the Jacobian without first deriving the forward kinematics model (FKM).

We saw how to do that in class, so here is the answer:

\mymatrix{H}^{0}_{2} = \left[\begin{array}{ccc} \cos{(q_0 + q_1)} & -\sin{(q_0 + q_1)} & l_{0}\cos{q_0} + l_{1}\cos{(q_0 + q_1)}\\ \sin{(q_0 + q_1)} & \cos{(q_0 + q_1)} & l_{0}\sin{q_0} + l_{1}\sin{(q_0 + q_1)}\\ 0 & 0 & 1 \end{array}\right].

(6)

This means that, from inspection,

\begin{align} p_{x}&=l_{0}\cos{q_0} + l_{1}\cos{(q_0 + q_1)} \\ p_{y}&=l_{0}\sin{q_0} + l_{1}\sin{(q_0 + q_1)} \\ \phi_{z}&=q_0 + q_1 .\\ \end{align}

(7)

Step 2: Calculate the differential kinematics by hand¶

We first calculate the Jacobian by hand, because programmatically there’s nothing for you to do yet.

The analytical Jacobian is given by

\mymatrix{J} = \left[\begin{array}{ccc} \frac{\partial p_{x}}{\partial q_0} & \frac{\partial p_{x}}{\partial q_1} \\ \frac{\partial p_{y}}{\partial q_0} & \frac{\partial p_{y}}{\partial q_1} \\ \frac{\partial \phi_{z}}{\partial q_0} & \frac{\partial \phi_{z}}{\partial q_1} \end{array}\right].

(8)

As we did in class, we find each element by calculating the partial derivative of the respective task-space value with respect to the configuration-space value

\begin{align} \frac{\partial p_{x}}{\partial q_0} &= -l_{0}\sin{q_0} - l_{1}\sin{(q_0 + q_1)} \\ \frac{\partial p_{x}}{\partial q_1} &= -l_{1}\sin{(q_0 + q_1)} \\ \frac{\partial p_{y}}{\partial q_0} &= l_{0}\cos{q_0} + l_{1}\cos{(q_0 + q_1)} \\ \frac{\partial p_{y}}{\partial q_1} &= l_{1}\cos{(q_0 + q_1)} \\ \frac{\partial \phi_{z}}{\partial q_0} &= 1 \\ \frac{\partial \phi_{z}}{\partial q_1} &= 1 \end{align}

(9)

resulting in

\mymatrix{J} = \left[\begin{array}{ccc} -l_{0}\sin{q_0} - l_{1}\sin{(q_0 + q_1)} & -l_{1}\sin{(q_0 + q_1)} \\ l_{0}\cos{q_0} + l_{1}\cos{(q_0 + q_1)} & l_{1}\cos{(q_0 + q_1)} \\ 1 & 1 \end{array}\right].

(10)

Step 3: Calculate the Jacobian in your code¶

We’re now equipped to solve the first question by doing the following

# Sample values, the particular values do not matter
q_0 = pi / 4
q_1 = pi / 3
l_0 = 0.2
l_1 = 0.1

# To possibly make it easier for you to read
J_1_1 = -l_0 * sin(q_0) - l_1 * sin(q_0 + q_1)
J_1_2 = -l_1 * sin(q_0  + q_1)
J_2_1 =  l_0 * cos(q_0) + l_1 * cos(q_0 + q_1)
J_2_2 =  l_1 * cos(q_0 +  q_1)
J_3_1 = 1
J_3_2 = 1

J = np.array(
        [[J_1_1, J_1_2],
         [J_2_1, J_2_2],
         [J_3_1, J_3_2]]
)

print(f"The analytical Jacobian at {q_0} and {q_1} is {J}")

The analytical Jacobian at 0.7853981633974483 and 1.0471975511965976 is [[-0.23801394 -0.09659258]
 [ 0.11553945 -0.0258819 ]
 [ 1.          1.        ]]

With the correct definition of the Jacobian as above, we can calculate the second question as

q_dot = np.array(
        [[5],
         [10]]
)

x_dot = J @ q_dot

print(f"In these conditions, x_dot = {x_dot}")

In these conditions, x_dot = [[-2.15599552]
 [ 0.31887821]
 [15.        ]]