L3 Forward Kinematics - OXBR Website

License: CC-BY-NC-SA 4.0

Author: Murilo M. Marinho (murilo.marinho@manchester.ac.uk)

Pre-requisites for the learner¶

The user of this notebook is expected to have prior knowledge in

All the content and pre-requisites of lessons 1 and 2.

I found an issue¶

Thank you! Please report it at https://github.com/MarinhoLab/OpenExecutableBooksRobotics/issues

Latex Macros¶

$\providecommand{\myvec}[1]{{\mathbf{\boldsymbol{{#1}}}}}$ $\providecommand{\mymatrix}[1]{{\mathbf{\boldsymbol{{#1}}}}}$

\providecommand{\myvec}[1]{{\mathbf{\boldsymbol{{#1}}}}}
\providecommand{\mymatrix}[1]{{\mathbf{\boldsymbol{{#1}}}}}

Pre-requisites¶

%%capture
%pip install numpy
%pip install numpy --break-system-packages

Imports¶

import numpy as np
from math import pi, sin, cos

Suggested exercises¶

What about an RRR robot?
What about if the robot had n degrees-of-freedom?
What if the robot is RP, that is, has a prismatic joint?

2 DoF planar robot (RR)¶

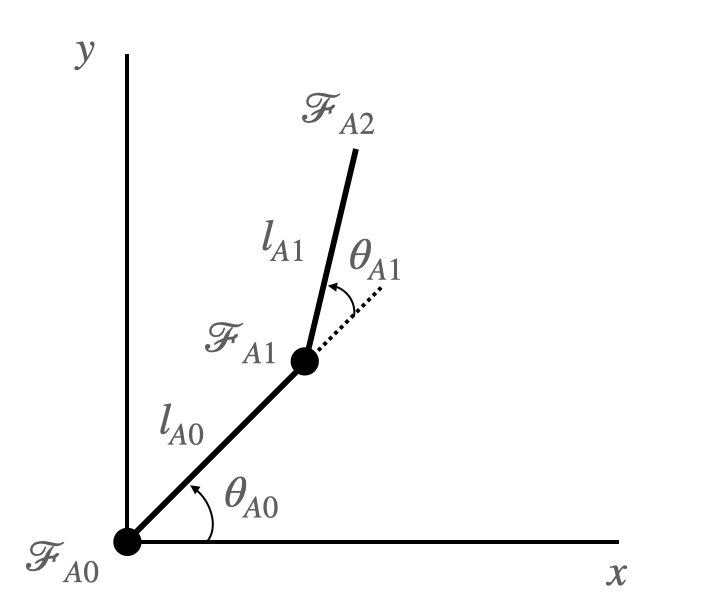
For the 2-DoF planar robot shown in the figure, use $\theta_{A0}$ , $\theta_{A1}$ , $l_{A0}$ , $l_{A1}$ to calculate

\mymatrix{H}_{A1}( \theta_{A0},l_{A0} ) \in SE(3)

(1)

and

\mymatrix{H}_{A2}( \theta_{A0}, l_{A0},\theta_{A1},l_{A1}) \in SE(3),

(2)

given that the pose of $\mathcal{F}_{A0}$ is $SE(3) \ni \mymatrix{H}_{A0} \triangleq \mymatrix{I}_4$ .

Understanding the problem¶

There is not much we can do without understanding what is being asked. In this regard, it is important to read and understand as much as possible the content already given. The programming part is extremely simple after the math is understood.

As described, the problem in question is that, for each joint transformation, we have a rotation followed by a translation.

The transformation of the first joint¶

\myvec H_{A1}^{A0}\left(\theta_{A0}\right) =\begin{bmatrix}\mymatrix R\left(\theta_{A0}\right) & 0\\ \myvec 0 & 1 \end{bmatrix}\begin{bmatrix}\mymatrix I & \begin{bmatrix}l_{A0}\\ 0 \end{bmatrix}\\ \myvec 0 & 1 \end{bmatrix}.

(3)

Programatically, supposing that $\theta_{A0} = \pi/4$ and $l_{A0}=0.3$ and if we define the initial rotation as $\mymatrix{H}_{R,A0}$ , we have

# Defining the rotation for A0. Note the correct syntax and, if well spaced, how easy it is to read
H_R_A0 = np.array(
        [[cos(pi/4), -sin(pi/4),  0,    0],
         [sin(pi/4),  cos(pi/4),  0,    0],
         [0,         0,           1,    0],
         [0,         0,           0,    1]]
)

print(f"The rotation is\n\n H_R_A0 = \n{H_R_A0}")

The rotation is

 H_R_A0 = 
[[ 0.70710678 -0.70710678  0.          0.        ]
 [ 0.70710678  0.70710678  0.          0.        ]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]

and if we define the translation as $\mymatrix{H}_{T,A0}$ , programmatically we have

H_T_A0 = np.array(
        [[1, 0, 0, 0.3],
         [0, 1, 0, 0],
         [0, 0, 1, 0],
         [0, 0, 0, 1]]
)

print(f"The translation is\n\n H_T_A0 = \n{H_T_A0}")

The translation is

 H_T_A0 = 
[[1.  0.  0.  0.3]
 [0.  1.  0.  0. ]
 [0.  0.  1.  0. ]
 [0.  0.  0.  1. ]]

hence

# When using numpy, the multiplication is done using the @ mark
H_A0_A1 = H_R_A0 @ H_T_A0

print(f"The first joint transformation is\n\n H_A0_A1 = \n{H_A0_A1}")

The first joint transformation is

 H_A0_A1 = 
[[ 0.70710678 -0.70710678  0.          0.21213203]
 [ 0.70710678  0.70710678  0.          0.21213203]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]

The transformation of the second joint¶

The second joint is, aside from parameters, the same as the first. Hence, the relative transformation is calculated similarly

\myvec H_{A2}^{A1}\left(\theta_{A1}\right) =\begin{bmatrix}\mymatrix R\left(\theta_{A1}\right) & 0\\ \myvec 0 & 1 \end{bmatrix}\begin{bmatrix}\mymatrix I & \begin{bmatrix}l_{A1}\\ 0 \end{bmatrix}\\ \myvec 0 & 1 \end{bmatrix}.

(4)

Programatically, supposing that $\theta_{A1} = -\pi/14$ and $l_{A0}=0.95$ and if we define the initial rotation as $\mymatrix{H}_{R,A1}$ , we have

H_R_A1 = np.array(
        [[cos(-pi/14), -sin(-pi/14),  0,    0],
         [sin(-pi/14),  cos(-pi/14),  0,    0],
         [0,            0,            1,    0],
         [0,            0,            0,    1]]
)
print(f"The rotation is\n\n H_R_A1 = \n{H_R_A1}")

The rotation is

 H_R_A1 = 
[[ 0.97492791  0.22252093  0.          0.        ]
 [-0.22252093  0.97492791  0.          0.        ]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]

and if we define the translation as $\mymatrix{H}_{T,A1}$ , programmatically we have

H_T_A1 = np.array(
        [[1, 0, 0, 0.95],
         [0, 1, 0, 0 ],
         [0, 0, 1, 0 ],
         [0, 0, 0, 1 ]]
)

print(f"The translation is\n\n H_T_A1 = \n{H_T_A1}")

The translation is

 H_T_A1 = 
[[1.   0.   0.   0.95]
 [0.   1.   0.   0.  ]
 [0.   0.   1.   0.  ]
 [0.   0.   0.   1.  ]]

hence, the relative transformation is

H_A1_A2 = H_R_A1 @ H_T_A1

print(f"The second joint transformation is\n\n H_A1_A2 = \n{H_A1_A2}")

The second joint transformation is

 H_A1_A2 = 
[[ 0.97492791  0.22252093  0.          0.92618152]
 [-0.22252093  0.97492791  0.         -0.21139489]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]

The final transformation¶

The problem is quite simple to solve after the relative transformations are known.

We know that

\mymatrix{H}_{A1}( \theta_{A0},l_{A0} ) = \mymatrix{H}^{A0}_{A1}

(5)

and that

\mymatrix{H}_{A2}( \theta_{A0}, l_{A0},\theta_{A1},l_{A1}) = \mymatrix{H}^{A0}_{A1}\mymatrix{H}^{A1}_{A2}

(6)

hence

H_A1 = H_A0_A1
H_A2 = H_A0_A1 @ H_A1_A2

print(f"The first transformation is\n\n H_A1 = \n{H_A1}")
print(f"The second transformation is\n\n H_A2 = \n{H_A2}")

The first transformation is

 H_A1 = 
[[ 0.70710678 -0.70710678  0.          0.21213203]
 [ 0.70710678  0.70710678  0.          0.21213203]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]
The second transformation is

 H_A2 = 
[[ 0.8467242  -0.53203208  0.          1.01652002]
 [ 0.53203208  0.8467242   0.          0.71756251]
 [ 0.          0.          1.          0.        ]
 [ 0.          0.          0.          1.        ]]

[Basic] Robotics using numpy

L2 Rigid Body Motion

[Basic] Robotics using numpy

L4 Differential Kinematics